Blog creado para todos aquellos que quieren conocer más profundamente sobre la filosofía y metodología de María Montessori.
jueves, 30 de enero de 2014
lunes, 27 de enero de 2014
domingo, 26 de enero de 2014
3.3 Juego del “yo veo”
Material:
Una charola con varios objetos. (La guía se asegura
que el niño conozca el nombre de todos esos objetos) Los objetos de la charola
son como mínimo 5 y máximo 10.

Presentación:
Puede hacerse en la mesa o en el tapete, es un juego
de grupo.
La guía comenta:
- Ese juego es
el de “yo veo”.
- Voy a darles
una seña para que ustedes identifiquen el objeto que yo estoy describiendo.
-Veo un objeto que tengo en mi mano que empieza con la
letra “c”. El niño, responde que es un “cubo”. Así les describes todos los
objetos de tu charola.
Variación:
Primer tiempo:
Veo, veo en mi mano… un objeto cuyo nombre empieza con
el sonido “c” y termina con el sonido “o”. El niño responde que cubo. Así les
describes todos los objetos de la charola.
Segundo tiempo:
Pones los objetos en el tapete.
Veo, veo en el tapete un objeto cuyo nombre empieza
con el sonido “c” y termina con el sonido “o”.
Tercer tiempo:
Pones los objetos en la mesa.
Veo, veo en la mesa un objeto cuyo nombre empieza con
el sonido “c” y termina con el sonido “o”. ¿Cuál es? Cubo. ¿Qué otros sonidos
escuchas? “u” y “b”.
De acuerdo al nivel de los niños, puedes enfatizar en
cada tiempo.
Control de error:
Sentido auditivo del niño, que se va desarrollando.
Propósito directo:
Darse cuenta de los sonidos.
Propósito indirecto:
Ayudar a la pronunciación correcta. Preparación
directa para la escritura. Exploración del sonido del lenguaje.
Nota: para este nivel todas las presentaciones deben ser
más ágiles.
3.2 Letras de lija
Material:
Son tablas de formaica o, madera que sea
particularmente lisa para que resalte la letra que va a estar adherida y que es
de lija. Las tablas están en dos colores diferentes para distinguir las vocales
de las consonantes. Hay dos medidas, una para las letras cortas y otra para las
largas. Incluye todas las letras del alfabeto de letras manuscritas y
minúsculas. Las consonantes van en color rosa y las vocales en azul. Una caja
de madera para guardar las letras. Material para suavizar las yemas de los
dedos que consta de una tela de terciopelo o gamuza, adherida a una pequeña
tabla.

Presentación:
Se trabaja en grupo, identificando a los niños que
todavía no conocen bien las letras.
Se inicia platicando la historia del alfabeto,
retomando algunos puntos de la historia. Con esta caja tan pequeña podemos
escribir todas las palabras que queremos.
Vamos a escoger de las letras de color azul (vocales)
y se les pregunta ¿Cuáles conoce?
En taller se presentan las que se asemejan.
Tocamos la letra y decimos “o”, pasamos la letra a
cada niño de grupito, la toca y repite el sonido de la letra.
¿Conoces alguna palabra que inicie con este sonido?
Ojo, oreja, hormiga, si, pero ésta palabra lleva una letra antes que después la
vamos a presentar.
Lo invitas a que trace en el aire la letra y la
repitan.
Se hace lección de tres tiempos. Primero se presentan tres
vocales y una consonante.
Las consonantes se presentan igual que las vocales y
también de tres en tres; después se da lección de tres periodos.
Se empiezan a formar palabras. Para formar palabras
primero con las letras de lija y luego con el alfabeto móvil grande. Las letras
de lija se ocupan para la primera ocasión.
Segunda sesión:
En una segunda sesión, retomas las vocales y buscas
una consonante que combinada con esas vocales puedan formar palabras.
Tocas y dices el sonido de la consonante, la pasas al
grupo y los niños tocan y repiten el sonido. Hacen la lección de tres tiempos.
Acercas tu caja del alfabeto móvil. Acomodas el alfabeto con los signos de
puntuación.
Se le pregunta al niño: Con esas letras que ya
conoces, ¿qué palabra puedes formar?
Si se presenta una palabra con acento y le das la
introducción del acento, le dices que una letra lleva más énfasis y le cambias
“a” por “á”.
Haces el análisis de sonidos, m…a, ma. (Nota: Es
importante que el niño tenga éxito inmediato, que pueda leer la palabra).
A los niños que no saben leer les presentas el
alfabeto grande y a los que ya saben leer les presentas el alfabeto móvil.
(Ese material se pide prestado a Casa de los Niños).
Propósito directo:
Conocimiento de las letras por su sonido y preparación
de la mano para la escritura.
Nota: Debe hacerse mucho análisis de sonido.
Edad: Cuando recibes a un niño que no sabe leer.
III.- Material de preparación para la escritura 3.1 Resaques metálicos
Material:
Resaques metálicos: 10 marcos de 14x14 cm., resaques
de círculo, pentágono, trapecio, elipse, rectángulo, cuadrado, triángulo, triángulo
curvilíneo, óvalo y tetrafolio. Cada uno de estos con una perilla central.
Material de dibujo: Protector de madera de 14x14 cm.,
hojitas de colores de la misma medida, lápices de colores con punta afilada y
portalápices.

Presentación:
Acompañamos al
niño a elegir uno de los resaques y que lo transporte a su mesa, lo mismo que
el material de escritura. Es posible en taller que cada niño tenga sus colores
en su cajón, en ese caso le pedimos que elija tres y le saque punta afilada.
Tomamos el marco con su resaque y lo colocamos en la
parte superior de la mesa, los colores en el portalápices al lado superior
derecho y el protector y la hoja en la parte central de la mesa.
Primero colocamos el marco sobre la hoja haciéndolo
coincidir exactamente. Pedimos al niño que tome uno de los colores y con él
trazamos el contorno de la figura con un solo trazo; devolvemos el marco a su
sitio.
Después tomamos el resaque con los dedos P:M:I
(Pulgar, medio, índice) y lo colocamos en el contorno ya dibujado. Y utilizando
otro de los colores trazamos su perímetro con un solo movimiento. Regresamos el
resaque y decimos al niño que con el tercer color llenaremos la superficie. Con
la mano en el aire y el movimiento de todo el brazo hacemos unos cuantos trazos
continuos de arriba hacia abajo con el primer contorno como límite. Pedimos al
niño que continúe con el trazado.
 |
Punto de interés:
El color y la forma.
Control de error:
Que sus dos contornos estén separados y que al
colorear no se salga de la figura.
Propósito directo:
Coordinación fina. Educación del ojo a una composición
geométrica y cronométrica. Adquirir control sobre su mano en el uso de un
instrumento o útil para escribir. Adquirir ligereza y mantenerse dentro de
cualquier límite,
Propósito indirecto:
Caligrafía y preparación para el trazo de letras. Se
refuerza indirectamente el concepto de superficie y el concepto de perímetro
cuando se traza el contorno.
Ejercicio grupal:
Durante los primeros meses del año podemos hacer
ejercicios grupales de resaques una o dos veces por semana. Cada niño prepara
su material, eligen la, o las figuras que desee, marca los contornos y las
devuelve al estante. Mientras colorean es posible estar en silencio.
Ejercicio siguiente:
Se realiza con el mismo material y consiste en colocar
el resaque sobre el papel y con un color delinear el contorno. Se observa la
figura trazada.
Nuevamente se coloca el resaque sobre el papel
cambiando su posición y con otro color se delinea el contorno.
Se rellenan los espacios pequeños, no se dibuja la
intersección.
Variaciones:
a)
Adornar el contorno de la figura. Decorar los ángulos.
b)
Se toman dos resaques que se delinean cada uno con un
color diferente. Se rellena el espacio entre las dos figuras.
c)
Cualquier variación creativa que al niño se le ocurra.
d)
Se utilizan tres resaques con la misma técnica.
e)
Se rellenan las figuras en diferentes formas, por
ejemplo: línea vertical recta, líneas curvas, zigzag, puntos, áreas oscuras y
claras, sombreadas, fuertes y suaves, etc.
f)
Usar papel más grande 20x20 cm. El procedimiento es
igual, únicamente varía el tamaño del papel.
Nota:
Es importante ayudar al niño a perfeccionar el
trabajo. Hacer puntos de conciencia para arreglar errores. Observar cómo el
niño toma el lápiz y hacer énfasis en la postura correcta al sentarse y la
posición del papel.
III.- Introducción a la lectura 3.1 Historia del papel que habla
Presentación:
Reunimos a los niños, les contamos la siguiente
historia:
“Hace muchos, muchos años, llegaron los españoles a
nuestro continente y se establecieron en varios lugares de nuestro país, allí
formaron misiones. Las misiones eran lugares en los cuales un grupo de
indígenas estaba al cuidado de una familia española que les proporcionaba
alimento y vivienda, y a cambio los indígenas trabajaban para ella.
En una de las misiones un español tenía plantados
varios árboles de peras. Un día mandó a su hijo con uno de los sirvientes
indígenas a cortar 10 peras de su primera cosecha y las colocó en una canasta,
la llevaron al español, el cual escribió en un papelito: Te mando diez peras de
mi primera cosecha y todos mis saludos. Dobló el papelito, lo colocó en la
canasta y mandó al sirviente a casa de su amigo a llevarle su regalo.
El camino era muy largo, y como hacía mucho calor, el
indígena tenía hambre y cansancio. Se sentó debajo de un árbol y cuidando de
que no lo viera nadie se comió una pera. Al rato siguió su camino hasta la casa
del amigo de su amo y le entregó la canasta. El español vio el papelito, contó
las peras y le dijo al indígena que se había comido una pera. Éste se
sorprendió muchísimo y regresó a su casa.
En otra ocasión el español le pidió al indígena que
llevara otra canasta que contenía veinte peras y un papelito. El indígena
emprendió su camino y cuando se cansó se paró bajo un árbol y observó que nadie
lo viera, pero para estar más seguro caminó 30 pasos a la redonda. Recordó que
después de leer el papelito fue cuando le dijo que se había comido una pera,
así que pensó que el papel podía tener algo que ver en que lo hubieran
descubierto la vez anterior, tomó el papelito y lo puso debajo de una piedra
mientras se comía dos peras. Tomó el papelito de debajo de la piedra y lo puso
en la canasta nuevamente antes de continuar su camino. Al entregar el encargo,
el amigo del español vio el papelito, contó las peras y le dijo que esta vez se
había comido dos peras. El indígena se sorprendió tanto que regresó rápidamente
a su casa y le preguntó al español: ¿Cómo es que ese papel puede hablar?
Así surgió en él un gran interés en aprender a leer y
escribir.”
Propósito Directo:
Compartir con los niños, a través del cuento, algo
sobre la utilidad de la lectura.
Propósito indirecto:
Despertar en los niños el interés por la lectura y la
escritura.
2.2 La historia del buey y la casa
Introducción:
La guía le comenta a los niños: Hace muchos
años, era difícil comunicarse; hoy es más fácil.
Para ello usamos el alfabeto. Con los símbolos del
alfabeto, podemos escribir ¡Cualquier palabra! ¡Cualquiera!
Ahora, te voy a explicar lo que significa la palabra
“alfabeto”. Esta es la historia del buey y la casa.
Material:
Cartelón con el alfabeto griego, fenicio y romano;
papel protector y plumón.
Presentación:
Reunimos a los niños y hacemos alusión a la función de
los pictogramas como medios de comunicación entre los hombres prehistóricos y
cómo en nuestro juego, vimos que los dibujos se prestaban a distintas
interpretaciones.
Hace muchos años hubo una región llamada “Fenicia”.
Los fenicios eran comerciantes; se dedicaban a comprar y vender cosas, por lo
cual tenían que viajar mucho. Tenían grandes barcos y eran excelentes
navegantes. Incluso lograron llegar a regiones tan distantes como “Sicilia”.
En ese entonces, la escritura se hacía por medio de
dibujos, pero los fenicios, siendo comerciantes, deseaban hacer las compras más
rápido, para lo cual inventaron algunos símbolos. Uno de estos símbolos representaba
un buey, porque cuando se mataba a uno de ellos, la cabeza se colgaba en algún
lugar alto, con los cuernos hacia abajo. Para mantener los cuernos separados,
la gente colocaba un palo entre ellos así: “A”. Este es el símbolo que los
fenicios usaron para buey. Buey se decía en fenicio “Aleph”; después de un
tiempo los griegos llamaron a este signo “alfa” y nosotros lo llamamos
actualmente “A”.

Existe también otro símbolo que representa la casa
egipcia: b, que se llamaba “Beth”; en griego lo llamaron “Beta” y para nosotros
es sólo “B”. Este fue el inicio del alfabeto, se llama así, por el nombre griego
de las dos primeras letras.

El alfabeto después se difundió por todo el mundo. Uno
de los primeros libros escritos, que además fue escrito a mano, fue la Biblia,
traducida en todos los idiomas y llevada después a todos los hombres. Los
fenicios llevaron el alfabeto a Palestina, de ahí se difundió a todo el mundo.
El primer punto donde se difundió fue en Grecia, por eso se tomaron los nombres
de las dos primeras letras para darle el nombre al alfabeto.”
Nuestro abecedario se deriva del griego y del latín, y
consiste en un signo para cada sonido.

Mostramos el cartelón a los niños y con ellos vamos
analizando los cambios de cada signo y su significado. Les comentamos que todas
las letras están relacionadas con cosas que eran importantes para la gente y
que de sus necesidades van surgiendo sus inventos.

Sin la escritura, todas aquellas civilizaciones se
hubieran perdido. Muchos libros se han perdido porque un pueblo destruyó la
cultura de otro; por ejemplo, los romanos destruyeron Cartago, que en su tiempo
tenía las mejores bibliotecas del mundo; lo mismo sucedió con Alejandría. Un
rey antiquísimo, Azurbanipal, también mandó a
hacer una biblioteca de piedra en la capital del pueblo asirio: Nínive pero
que también fue destruida. Muchas tablas que contienen estos símbolos han sido encontradas
recientemente por los arqueólogos.
Propósito directo:
Despertar el interés de los niños por los logros
humanos surgidos de la creatividad para satisfacer sus necesidades.
Propósito indirecto:
Dar a los niños el desarrollo del lenguaje escrito.
2.1 Historia del lenguaje escrito
Material:
Crayolas, papel, protectores, carteles con pictogramas
y pinturas rupestres.
Presentación
La guía platica a los niños, cómo los hombres de antes
recordaban hechos importantes a través de la transmisión oral del mensaje, de
unos a otros, de viejos a jóvenes.
Pregunta a los niños que podría suceder algunas veces
en la transmisión oral de dichos mensajes. El niño concluirá que muchas veces
éstos se distorsionaban.
La guía explicará en este punto, cómo surgen las
leyendas (mensajes distorsionados). Se pueden escoger dos o tres leyendas de
diferentes pueblos, que leeremos con ellos.
Se pregunta a los niños qué creen que hicieron los
hombres para evitar que los mensajes se distorsionaran. Se induce a los niños a
concluir que, surge entonces, la necesidad de escribir los mensajes.
El hombre escribe a través de dibujos. Dibujos que
representan cosas de la naturaleza o fenómenos naturales. Dibuja en las rocas,
en los troncos de los árboles, en las paredes delas cuevas.
Se invita a los niños a escoger un objeto y a
representarlo mediante un dibujo.
Se retoman los dibujos y se genera un mensaje,
ordenándolos.
Pudiera cada niño ordenar los dibujos a su parecer;
invitar a los demás a interpretar su mensaje y al final, el niño, expresará el
mensaje inicial.


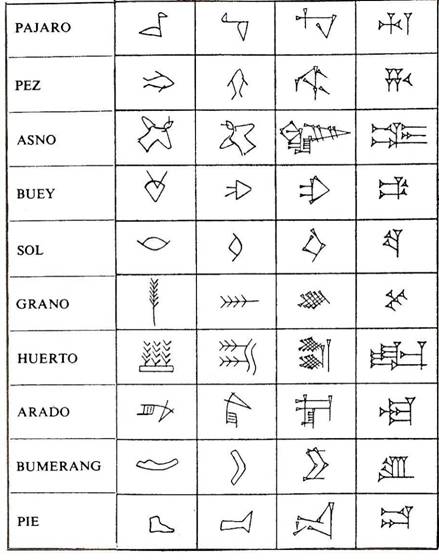
La guía menciona a los niños que: A través de muchos años estos dibujos se han hecho más sencillos. A este tipo de escritura se le llama: Pictográfica o Pictografía.-
(Estas pictografías se encontraron en Montreal Canadá.
El libro que contiene su interpretación se llama Moorhouse.)
En Egipto llegaron a simplificar mucho su escritura.
La escritura egipcia más antigua se llamó: jeroglífica. Sólo algunas personas
llamadas escribas la conocían.
Después hicieron otra menos elaborada llamada
hierática y por último a las más simple la llamaron demótica, para que finalmente
una gran parte del pueblo pudiera leerla.
Propósito directo:
Juego de integración y expresión.
Propósito indirecto:
Introducción al desarrollo del lenguaje escrito.
sábado, 18 de enero de 2014
Números de lija
Material:
1. Un tapete o mesa
2. Una caja con números de lija del 0 al 9

Presentación:
Se invita al niño
a tomar el material, se presentan de dos en dos, dando lección de tres tiempos.
Nota: El niño de taller ya
conoce los números de lija ya que los vio en casa de los niños.
Taller:
Se colocan los
números en el tapete al azar y el niño los ordena del 0 al 9, en orden. En
forma ascendente o descendente.
Introduciendo el
concepto y el lenguaje; “antecesor y sucesor”, “mayor que y menor que” y “pares
o nones”.
Propósito:
Repasar en taller
los símbolos correspondientes de las cantidades conocidas.
La secuencia de la
colocación de los números y un trazo correcto.
Los dones
Esta Presentación es
para hacer una entrega simbólica de las bases que se lleva de un colegio
Montessori para toda la vida, que son los números y las letras.
Esta presentación
se les da a los niños en su entrada o salida del taller:
Material:
1. Letras de lija
2. Números de lija
3. Tela oscura

Presentación: Con todos
los niños reunidos, se les habla muy solemnemente y con mucha seriedad.
“Hoy, les hago
entrega de un legado, el cual deben atesorar en lo más valioso de su corazón,
estos dones que no tienen y que pronto tendrán, y los que ya los tienen
también.
Estos dones les
servirán de ahora en adelante y por siempre, como el más fiel de los amigos,
ellos te ayudarán a superarte, a ser inteligente y culto; te abrirá las puertas
de la imaginación y la creatividad”.
Se destapan las
letras y los números de lija.
Propósito: Introducir al
niño con las herramientas que le van a servir para el trabajo, explorar y
conocer su alrededor. Maravillar al niño con el trabajo de los hombres que nos
precedieron. Despedir a los niños de taller y que vean que gracias a estos dos
instrumentos pudieron trabajar y aprender.
Presentaciones de introducción de las matemáticas
DESARROLLO DE LAS MATEMÁTICAS
Para
que exista una comprensión clara y concreta de las matemáticas, se necesita
tener una previa experimentación de la esencia de las cosas por medio de los
sentidos.
De
6 a 12 años, se desarrolla la capacidad de conciencia del conocimiento,
realizando una importante relación de la esencia de la abstracción.
La reversibilidad
es una habilidad que el niño puede obtener a través del uso del material
concreto, y consiste en entrar y salir de una abstracción, por ejemplo:
10 unidades = 1
centena
1 decena = 10
unidades
Después de este
análisis se logra la síntesis.
María Montessori,
explica que la reversibilidad es un cierre de ciclos, logrando una salud
mental, por ejemplo:
Los egipcios
utilizaban los números, los cuales crearon a partir de lo que conocían y de
acuerdo a sus necesidades.
El trabajo de una
guía es seducir al niño para sacarlo del mundo, atraerse de un material y
abstraer un conocimiento.
El trabajo está
ligado con la creatividad del niño.
Uno de los
descubrimientos de María Montessori, era que hay una potencialidad en la
personalidad del niño, que corresponde a todos esos fenómenos universales,
dirigiendo al niño en crecimiento a realizar actividades específicas.
Al niño se le
puede introducir a las matemáticas por medio de su propio cuerpo, midiendo,
experimentando y creando ejercicios nuevos prácticos para él.
PROPORCIÓN
DEL CUERPO Y EL USO DE LAS MATEMÁTICAS
El niño debe
aprender a experimentar con las matemáticas, no quedarse solo con los números
sino comprobar.
Material: Estambre
o hilo nylon.
Presentación: Con
un hilo el niño va midiendo su cuerpo, pero debe de tomar relaciones del mismo,
ejemplo: La mano abierta desde el dedo gordo al dedo índice.
EJERCICIOS
CON LAS MANOS PARA DESARROLLAR LAS TABLAS DE MULTIPLICAR
Tablas del 6 al 10
|
|
Mano izquierda Mano
derecha
Con
las manos de frente, se le da diferente denominación a los dedos:
·
Pulgar =10
·
Índice =9
·
Cordial =8
·
Anular =7
·
Meñique =6
La multiplicación
se va a resolver del siguiente modo:
A partir de los
dedos que se unen, los dedos superiores son los de la izquierda, el producto se
suma con las decenas que corresponden a los dedos inferiores incluyendo los
dedos que se unan según sea el caso, ejemplo:
OTRA
FORMA DE MULTIPLICACIÓN PARA LA TABLA DEL OCHO
Se utilizan ambas
manos y el multiplicador es la mano que se dobla según la jerarquía que se
quiere aplicar.
A partir del dedo
que se doble, el producto que se encuentra al lado izquierdo son las decenas y
el lado derecho son las unidades que se multiplican por dos.
Después de
multiplicar por cinco se descuenta el pulgar de la mano izquierda para que el
producto de las decenas sea correcto, ejemplo:
OTRA
FORMA DE MULTIPLICACIÓN PARA LA TABLA DEL NUEVE
El
multiplicando es el número nueve y el multiplicador es el número del dedo
doblado, los dedos sobrantes del lado derecho a partir del dedo doblado, es el
producto de las unidades, se suman las decenas con las unidades dando el
producto total, ejemplo:
SUMAS
QUE DE PRODUCTO SIEMPRE DE QUINCE
Es
un juego en el cual, el niño puede pensar utilizar la imaginación que le
ayudará a resolver el ejercicio.
Las
reglas del juego es que en un cuadrado de 3 x 3
se realicen sumas de tres número, los cuales den como producto 15 de
cualquier forma que se le sume (horizontal, vertical y diagonal.
No
se debe repetir ningún número del 1 al 9.
Introducción a las matemáticas
Definición de Mente Matemática: Esa parte
exacta, ordenada y precisa de la mente humana. Está presente en el nacimiento y
tiene la potencialidad de realizarse si se le proporciona un ambiente propicio.
De una manera característica llega a operaciones y a considerar su ambiente
desde un punto de vista el cual podemos llamar matemático. El hombre, por
naturaleza mide y también por naturaleza razona, y ese medir y razonamiento es
matemático. Las matemáticas son la base de todas las ciencias, y como Pitágoras
las definió:
“…es
el campo más fascinante de la actividad humana. Es una expresión particular
básica, característica de la mente humana”.
El
lenguaje y las matemáticas son creaciones de la mente humana y en algunas
ocasiones su origen ha sido atribuido a un factor súper-humano.
Las
matemáticas no existen por si solas. Son una expresión de la mente humana. La
expresión y precisión son hechas por el hombre. Quizá la mente humana sea la
mejor y más grande herramienta en el Universo. Propio de ella es el orden y la
capacidad de extenderse hasta el infinito.
El
universo está regido por leyes, y en el plano físico mucho de esto puede
reducirse a ecuaciones matemáticas.
Está
en la naturaleza, pero el uso que le da el hombre está más allá de la
naturaleza, sin embargo cabe perfectamente en el reino del hombre. El
universo en su totalidad se comporta de acuerdo a principios matemáticos. La
lógica y razonamiento de las matemáticas ayuda al hombre a que descubra su mundo
y a que manipule ideas que él pueda tener. Aún las actividades más básicas de
la vida cotidiana requieren de las matemáticas para dar forma a nuestro
comportamiento en el ambiente.
Las
matemáticas entonces, requieren algo del pensamiento más profundo del hombre,
pero aun así, él no puede pasar ni un solo día sin utilizar las matemáticas de
alguna manera, ya que su uso es constante en todo el mundo.
Desde
el inicio de la historia del hombre él ha contado, medido, calculado,
planificado y predicho. Las matemáticas crecieron con la civilización.
Surgieron de problemas prácticos y ayudaron a resolverlos. En los días cuando
el hombre obtenía sus alimentos por medio de la caza y de la recolección de
frutas silvestres y de semillas, tenía que contar para llevar un control de sus
provisiones.
Sin
embargo, un proceso tan sencillo como el conteo (aparentemente) pasó por muchas
etapas antes de alcanzar un nivel que permitiera la sistematización.
El
concepto de cantidad llegó de una manera natural al hombre. En los tiempos más
remotos, el único tipo de matemáticas que él conocía era el conteo con los
dedos. Durante miles de años cantidades mayores de tres, se consideraban como
un montón o una pila-
No
tenían calendarios ni mapas. Tuvieron que aprender estas cosas lentamente, por
medio de largas experiencias ya través del intento y el error. Sólo tenían el
sol, la luna y las estrellas para guiarlos. La salida del sol y su ocaso
cambiaba de estación en estación, y las estrellas en una noche ofrecían una guía
confiable para encontrar la dirección. Para medir períodos de tiempo más
largos, nuestros ancestros deben haberse guiado por la luna. El tiempo vuela, y
el conteo de los días o de os meses no era como el contar venados o dientes de
oso. Resolviendo el problema haciendo una incisión en un árbol, y marcando con
una tajada o una piedra cada día que pasaba –treinta días entre una luna llena
y la siguiente, doce de éstas conformando rudimentariamente un año – el primer
calendario lunar-.
El contar, medir y
calcular se volvieron más importantes cuando el hombre se convirtió en pastor o
en granjero. Ahora las personas tenían que medir la tierra y contar sus
rebaños.
El hombre
primitivo, no teniendo unidades de medida fijas, ni monedas, ni comercio más
allá del trueque más rudimentario, ningún sistema de pago de impuestos y
ninguna necesidad más allá del hombre primitivo, no tenían la necesidad de
numerales escritos, hasta más o menos el comienzo de lo que llamamos tiempos
históricos. Algo mucho más importante para estos cazadores que en un
conocimiento de matemáticas, era el conocimiento de estas estaciones y sentido
de orientación, para poder así pronosticar cuándo las nueces y las bayas
empezaban a madurar en algún bosque lejano y/o los medios para poder orientarse
y llegar hasta allá.
El hombre comenzó a
contar por intuición, hace mucho tiempo y en los inicios de su historia
aprendió a disfrutar las formas, los tamaños y la simetría. Se inventaron
símbolos numéricos, y se consideró a los números tan maravillosos que éstos
comenzaron a tener un significado misterioso.
Se ha considerado
por mucho tiempo a las matemáticas como: “La ciencia de magnitud discreta y continua”,
y en este sentido el origen de Matemáticas y Geometría ciertamente es
Pre-histórico. Tales artefactos como la tarja paleolítica con hendiduras y
patrones neolíticos en la cerámica, muestran que la idea de base numérica y
nociones de congruencia y similitudes surgieron mucho antes que el arte de la
escritura.
De las 4 grandes
civilizaciones antiguas, sólo Babilonia y Grecia contribuyeron al desarrollo de
las matemáticas. De las épocas remotas del pueblo de Babilonia (1700 a. C.) hay
tablas de multiplicar, tablas de recíprocos y tablas de cuadros y cubos.
Durante este periodo se introdujo el sistema sexagesimal, una escala que aún
perdura en mediciones modernas de tiempo y ángulos.
La medición de
áreas figuró de manera prominente en las matemáticas egipcias, como era de
suponerse en el periódicamente inundado valle del Nilo. Algunos creen que existe
evidencia de pruebas matemáticas en el Egipto antiguo. La construcción de las
pirámides parecía algo imposible sin el conocimiento de algunos principios
matemáticos. Muchas pruebas geométricas provienen de los matemáticos Griegos:
Herodoto, Pitágoras, Euclides y Arquímedes.
Entre los años 800
y 100 a. C. las matemáticas estuvieron influenciadas por la civilización
musulmana. La astrología y numerología del Este estaban combinadas con el
tratamiento Geométrico y Filosófico de la teoría matemática del Oeste.
La aritmética
estudia los números y la geometría estudia el espacio. Para predecir el cambio
de estaciones, estudiaron el movimiento del sol, la luna y las estrellas. Los
navegantes también observaban el cielo y buscaban a las estrellas que los
guiaban de lugar a lugar.
Para ayudarse en
este trabajo el hombre inventó la trigonometría –La cual relaciona las
distancias con las direcciones-.
Se expandió el
comercio por todo el mundo. El mismo tipo de cálculos debía repetirse. Para
ganar tiempo, algunas personas pensaron en reglas para hacerlo, y en formas de realizar
varias operaciones al mismo tiempo. Este fue el inicio del Álgebra.
Conforme fueron
pasando los siglos, el hombre construyó máquinas y talleres. Los científicos
estudiaron la tierra, el aire y el cielo. En estas actividades los hombres
trabajaban con cosas que se movían o cambiaban. Para pensar con certeza sobre
el movimiento y el cambio, inventaron el cálculo. Nuevos tipos de trabajo
trajeron nuevos problemas, y el hombre inventó nuevas ramas de la ciencia para
poder resolverlos.
Una comprensión de
las matemáticas es una ayuda para trabajar con nuestro propio ambiente. Ya sea
pre-histórico, ultra-moderno, rico, pobre, viejo o joven, las matemáticas son
parte de y una ayuda para el desarrollo. Es una parte del desarrollo natural
del hombre. El hombre prehistórico lo hizo intuitivamente; y así también lo
hace el niño. Conforme crece el hombre y la humanidad, también debe crecer su
conocimiento y comprensión de las matemáticas. Un verdadero conocimiento de
éste puede ayudar en el proceso de desarrollo del hombre.
Los hindús fueron
los primeros en utilizar 10 números en el sistema de valor relativo. Esto lo
tomaron los árabes y al Khowarizmi lo puso por escrito en el año 800 a. C.,
este sistema fue transmitido a Europa en el siglo XIII.
Durante los dos
últimos siglos ha habido inmensos avances en matemáticas, los cuales pueden
compararse en su novedad y extensión con aquellos de las ciencias físicas.
Los numerales más
antiguos de los cuales tenemos un récord definitivo, son simplemente líneas
rectas para los números pequeños y alguna forma especial para el diez. Las
líneas verticales I, II, III, etc. posiblemente sean representaciones de los
dedos levantados que se utilizaban para contar, y en computación, una señal
lingüística donde se encuentra la palabra “DIGITO”.
Estos numerales
primitivos fueron utilizados de acuerdo a las necesidades de las gentes. La idea
de una figura de grupo seguro se le ocurrió a los mercaderes tan pronto se
desarrollaron los números mayores de 10 y 12 en Egipto y Babilonia. Una vez que
surgió la idea, probablemente influenciados por los diez dedos, se inventaron
símbolos para las unidades más pequeñas como en el caso de aquellas utilizadas
para el cuatro y el cinco. La idea de símbolos especiales para grupos mayores,
como 20, 30, etc., fue una extensión natural. Los griegos utilizaron, y aún lo
siguen haciendo, las letras de su alfabeto con un signo distintivo.
No hay lenguaje sin
términos para los numerales. La noción de unidad y pluralidad se expresa cuando
menos en la formación de “uno” y “dos”, aunque “dos es frecuentemente igual a
mucho”, así concluyendo una numeración que tan sólo ha comenzado.
Sólo el sistema
decimal parece haberse originado en el ciclo cultural de los grupos nómadas,
quienes al contar sus grandes rebaños de ovejas, manada de caballos, vacas y
camellos necesitaban utilizar números más grandes.
De los grupos nómadas,
este sistema se ha expandido por todas partes y se encuentra ahora en todas las
naciones. La invención de la numeración y la posición de los números en ésta se
considera una piedra milenaria en la historia intelectual de la humanidad. En
nuestro sistema decimal de numeración la base es 10, ya que la llave para todo
es el número 10.
Cuando se habla de
número, uno inmediatamente piensa en el estudio de la Aritmética. En su
significado original, la aritmética sí significaba la ciencia o teoría de los números,
pero ahora se considera generalmente como algo que concierne a la computación,
así que la aritmética es entonces el estudio matemático más elemental.
Las herramientas de
la aritmética son los números cardinales y ordinales. Uno, dos, tres, etc., son
números cardinales; Primero, Segundo, Tercero, etc., son números ordinales.
Matemáticas es una
ciencia basada en cantidades pensantes. En aritmética, las cantidades se
expresan en números y cada número puede escribirse utilizando diez símbolos.
Pero el número es una palabra amplia, ya que denota tanto un conjunto de
unidades abstractas como el símbolo que representa tal conjunto.
Generalmente es
aceptado que las razas primitivas y los niños pequeños no pueden concebir la
idea de una sucesión infinita de números naturales, pero sin embargo, son
capaces de asimilar la idea de una serie simple que termine, por ejemplo en 10,
con la cual ellos han adquirido un grado de familiaridad operativa.
Las matemáticas
como lenguaje representan una creación de la mente humana. Descubre y expresa
algo que existe en el ambiente. Para ser capaz de distinguir uno y más de uno,
se necesita la habilidad de abstraer. Aquí entonces podríamos encontrar el
origen de los problemas que las matemáticas pueden crear para el niño pequeño,
ya que la abstracción es un paso muy
grande que toma la mente humana, y que debemos permitir que el niño lo tome a
su tiempo. Si queremos anticipar este desarrollo en la mente del niño, sólo nos
engañaremos. Hacemos que el niño repita los nombres de los números y ya con
esto creemos que puede contar. Él sólo está repitiendo correctamente, tal y
como repite una canción. El aspecto cuantitativo es algo aparte.
Para que el niño
pueda comprender lo que es “cantidad” deberá alcanzar cierta madurez mental.
Esto debe hacerlo individualmente, cada niño. Nosotros no podemos hacer que lo
logre. Casi todos los idiomas tienen su propia rima para enseñar al niño los
nombres de cada número, pero esto no le da ninguna comprensión de “cantidad”
sin la cual el niño no podrá llevar a cabo las operaciones aritméticas.
Existen muchos
prejuicios acerca de cómo se deben enseñar al niño los números y que es
imposible el enseñarle. Es posible, pero no en la forma tradicional. Debemos
permitir que el niño alcance cierto nivel de desarrollo gradual. En determinado
momento, cuando al niño se le ha dado determinadas ayudas (ejercicios), viene
el despertar de la mente matemática. El paso de la sola exploración sensorial
en la base de impresiones, a una exploración la cual podemos denominar
medición. Él busca establecer relaciones exactas, no sólo en cantidad pero
también en el tamaño y forma, El comienza a preguntar ¿cuántos?, y desea una
respuesta precisa. Si no damos al niño los medios para encontrar la respuesta
precisa, él solamente podrá tener símbolos que no le aportarán una experiencia
completa.
El niño que llega a
este campo de actividad humana a su propio paso y tiempo y encuentra en ese
tiempo lo que le ayudó a entrar en él, lo hará con tanto entusiasmo y de manera
triunfal que mostrará qué tan falso es el mito que dice que la mente humana no
es matemática. De todas las actividades que ofrecemos al niño en casa de los
niños, ningunas son tan populares, tan capaces de inspirar entusiasmo,
intereses y concentración como las matemáticas.
El niño deberá
darse cuenta que cuando contamos determinados objetos tales como cuentas,
conchas, caracoles, no estamos hablando acerca de los objetos en sí, sino que
nos estamos refiriendo a algo acerca de ellos, su cantidad. Esta “cualidad”
abstracta tiene que “ser exteriorizada” y “vista” por la mente. Esta “cualidad”
debe ser vista como algo fuera/aparte de los objetos mismos.
Esto es sencillo
para el niño brillante, pero algunos sólo ven los objetos y se sienten confusos
con nombres nuevos y aparentemente irrelevantes. Podemos decir al niño, “tres
conejos”, pero cada uno de ellos es un conejo, así que ¿Cuál es el significado
de esta nueva palabra?
Si le damos los
medios adecuados el niño se fascinará con la posibilidad de establecer precisamente
cuántos, o qué tan pocos, qué tantos más, etc.
Los niños menores
de cuatro años pueden manejar cantidades menores de 10 sin ninguna dificultad.
Las dificultades psicológicas del conteo son, primero su significado, el cual
resolvió la Dra. Montessori con el material conocido como “material del sistema
decimal”.
Una vez que estas
dificultades de número hayan sido vencidas, abrimos para el niño el mundo de
los números para su exploración y el niño prosigue paso a paso con el mayor
entusiasmo, ya que el número es algo que viene al hombre de manera natural e
intuitiva. Hoy en día podemos ver la enorme importancia de la física matemática
acompañada por el desarrollo de computadoras altamente desarrolladas. Se vuelve
esencial en cada campo de la ciencia, para el químico, físico, astrónomo e
ingeniero. Entonces cada niño tiene el derecho a esta herencia de la humanidad,
aprendiéndola apropiadamente.
La preparación
indirecta para las matemáticas se ha dado con los ejercicios de vida práctica
por medio del:
·
Análisis lógico del movimiento
·
Presentaciones precisas y
ordenadas
·
Material en secuencias, en
presentaciones y progresiones
·
Control error
·
Trabajo ordenado
·
Control de error para la
verificación de la exactitud la cual lleva a la auto-perfección.
Con los materiales
sensoriales:
·
Claridad en la expresión-lenguaje
·
Percepciones precisas y exactas a
través de los ejercicios con figuras y formas.
·
Presentaciones precisas y uso
adecuado de los materiales
·
Materiales (hasta 10 en cantidad)
cuadrado, volumen, geometría.
Las cualidades y
características de los materiales de matemáticas tienen:
·
Exactitud: Necesitan ser exactos,
por medio de la verificación sólo una respuesta correcta para un problema, el
control de error y las presentaciones ordenadas.
·
Orden: Siguiendo un procedimiento
establecido, aumentando las dificultades conforme el niño va madurando sin
frustración.
·
Repetición: Necesario absorber
operaciones abstractas, a través de la práctica la cual lleva a la perfección.
Exploración y
orientación: Descubrir la interrelación entre números y operaciones. Se propone
una metodología precisa, el incorporar nueva información, expander habilidades
y el descubrimiento de limitaciones.
·
Abstracción: el material concreto
y las abstracciones materializadas proporcionan proceso para el desarrollo de
la abstracción y también proporcionan un proceso preciso para usar en las
operaciones.
·
Auto-perfección: matemáticas es
una herramienta que debe desarrollarse con la cual el individuo puede entonces,
llegar a un pensamiento lógico y ordenado lo cual permite logros posteriores.
Existen dos
conceptos básicos para este trabajo:
A.
Abstracciones materializadas, las
cuales comienzan con el material sensorial, la presentación concreta de los
conceptos y que cada paso en matemáticas gradualmente va descartando a las
“muletas materiales”.
B.
Aislamiento de la dificultad, solo
una dificultad se introduce a la vez. Cada dificultad previa se incluye en el
ejercicio siguiente. Cada paso debe ser comprendido en su totalidad antes de
que se presente una nueva dificultad. No se puede omitir ningún proceso sin
dejar una brecha en la comprensión.
Hay un
procedimiento de presentaciones las cuales siguen una progresión ordenada:
Números del 1 al 10: Esta área es para
presentar la cantidad, el símbolo y la secuencia de los números, introducirlos
y establecer las bases para el trabajo con el sistema decimal.
Barras numéricas.-
Introducción a la cantidad
Numerales de
lija.- Introducción al símbolo
Barras numéricas y
numerales.- Asociación de la cantidad y el símbolo. Secuencia numérica 1 – 10.
Caja de husos.-
Concepto de 0 como una entidad vacía. Secuencia numérica 1-9
Fichas y
numerales: comprensión del concepto pares y nones y de números con una cantidad
formada por unidades separadas y la divisibilidad de los números.
Juego de memoria
con números.- Prueba de la compresión del concepto.
Sistema decimal:
Esta área es para presentar el sistema decimal y las cuatro operaciones,
introducir números grandes, categorías y operaciones. Dar ejercicios colectivos
para una comprensión básica. Tener el juego de las estampillas y el juego de
los puntos para práctica individual y como una ayuda posterior para la
comprensión. El juego de los puntos es para la suma en columna y para el
“llevar”.
Paralelo al sistema
decimal está el área de las tablas de Seguin la cual es para presentar los
número del 1 – 99, la introducción de los números intermedios lo cual es un
prerrequisito para la memorización de las tablas y esto se logra por medio del
conteo lineal y de los ejercicios de conteo salteado.
El trabajo de
memorización, lleva a la exploración y memorización de las tablas de las cuatro
operaciones. Comienza con ejercicios concretos, sigue con la escritura en los
tableros, practica con las tablas de trabajo de operación y la prueba o
comprobación son las tablas ciegas de cada una. Sique con el pasaje a la
abstracción con las operaciones antes de eliminar materiales, y al final viene
la introducción a las fracciones y sus 4 operaciones introduciendo el hecho de
que es tan sencillo el trabajar con las partes de un número como el hacerlo con
el número completo.
Los primeros tres
años de la vida del niño están plenos de experiencias concretas las cuales
preparan indirectamente a la mente matemática dándose cuenta de las diferentes
propiedades de todo lo que le rodea. Cuando llega a la casa de los niños,
encuentra muchas experiencias más, las cuales lo preparan indirectamente. El
observa, experimenta y abstrae distinciones cada vez más finas de volumen,
forma, dimensiones, anchura, temperatura, clasifica y puede seguir un orden
secuencial y esto clasifica y ordena su mente y desarrolla sus conceptos
matemáticos.
El papel del
adulto, en esta área es muy importante. Primero deberá de eliminar experiencias
previas en matemáticas, las cuales pueden transmitirse a los niños. El es
responsable de las presentaciones en secuencia y el de estar alerta del
progreso y nivel de comprensión de cada niño. Deberá ser capaz por medio de su
práctica de comprender el material profundamente, y ser responsable de
proyectar al niño una buena imagen tanto en lenguaje y acciones como en
presentaciones.
“El
niño cuando nace, nace con potencialidad de una mente matemática que puede o no
desarrollarse según los estímulos que encuentra en los ambientes que se le
ofrezcan”.
De
0 a 3 años encontramos ejemplos en cada uno de sus movimientos, el horario
entre sus alimentos, sueño, cuando intenta alcanzar sus alimentos, juguetes,
cuando se mide con la mesa, etc.
El
niño es un ser inteligente y armónico y el orden es una necesidad para orientarse
en la vida y es la base de la eficiencia y como consecuencia de la independencia,
María Montessori dentro de su Filosofía de Vida, propone el manejo de las
matemáticas como un lenguaje necesario, natural y espontáneo, proporcionándonos
materiales como ella los llama “Abstracciones Materializadas” le permiten
observar, experimentar, analizar y hacer suyas las diferentes operaciones
matemáticas.
Relaciones:
menor que, mayor que, igual, diferente a, selección, clasificación, separación,
inclusión, seriación, pertenencia, reversibilidad, perspectiva,
proporcionalidad y lógica.
De
3 a 6 años esta mente matemática requiere de la información adecuada a través
de todos sus sentidos y en el ambiente Montessori de Casa de los Niños
encuentra todos los motivos de interés para esto.
Nosotros
vamos a tomar dos materiales que nos darán una visión muy amplia y que nos
muestran claramente la diferencia entre material didáctico (un momento de
interés) y de desarrollo (cada vez que lo experimentamos podemos deducir nuevos
conceptos).
Las
barras de colores: al principio el niño las clasifica por colores, después las
ordena, posteriormente hace secuencias, series ascendentes o descendentes,
encuentra relaciones, forma figuras, se inicia a operar.
De
6 a 12 años, el niño continua con esta experimentación y ahora en la formación
de conciencia encuentra las relaciones necesarias para operar, encontrar
propiedades y aplicarlas.
Como
observaremos ahora es capaz de hacer gráficas de diferentes fenómenos naturales
o sociales, ordenarlos según su importancia y clasificarlos.
Tiene
los esquemas de acción ya formados, por lo que simbólicamente puede
presentarlos y deducir principios de causalidad.
La
organización didáctica de todas las áreas de aprendizaje se interrelacionan
entre sí, adaptándose a las características e intereses de los niños y basados
fundamentalmente en su percepción sincrética.
En
la Educación Montessori a nivel Taller el trabajo se realiza generalmente en 4 etapas:
1. Observación
2. Experiencia
3. Análisis y comprensión
4. Abstracción
Y esto puedo
realizarlo por las características del material:
A. Es sensorial. Es visual (color, forma, dimensión). Es estereognóstico
(tridimensional).
B. Es creativo
C. Da una preparación indirecta
D. Son abstracciones materializadas
Nota: tomado de las clases con la Profesora Águeda
Vega
Suscribirse a:
Comentarios (Atom)